Tiefe Frequenzen = grosse Probleme

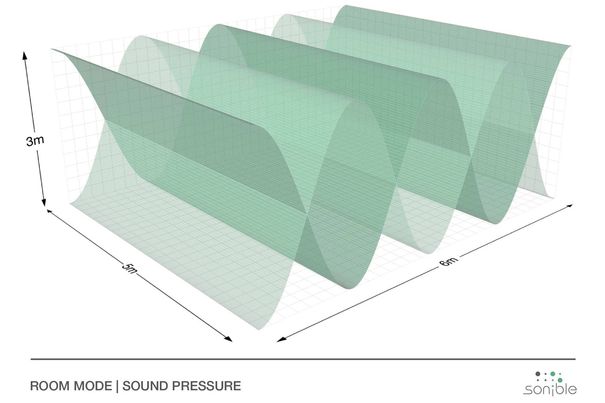Grafische Darstellung von Raummoden.

Wir wollen uns in diesem Artikel auf die «tiefen» Frequenzen konzentrieren, da diese die meisten Probleme verursachen (je nach Beschaffenheit der Wände, Decke, Boden können allerdings auch höhere Frequenzen Probleme verursachen). Die Frage ist, bis zu welcher oberen Frequenz gehen diese «tiefen», Probleme verursachenden Frequenzen? Diese obere Frequenz, die sogenannte Schröderfrequenz, lässt sich mit der folgenden Formel berechnen:

F = 2000 x √(T / V)

T ist die Nachhallzeit des Raumes in Sekunden, V das Volumen des Raumes in Kubikmeter. Die Nachhallzeit hängt oft mit dem Volumen zusammen, sodass für nicht zu hallige Räume die Frequenz F um die 300 Hz zu liegen kommt.

Was passiert nun bei diesen tiefen Frequenzen? Bei gewissen Frequenzen entstehen sogenannte stehende Wellen oder Raum-Moden. Das heisst, die Schallwelle passt in ihrer Länge schön in die Länge oder Breite oder Höhe des Raumes. Die Länge der Schallwelle berechnet sich mit:

L = c / f

c ist die Schallgeschwindigkeit im m/s, ca. 343 m/s, f ist die Frequenz in Hz.

Beispiel: Eine Frequenz von 100 Hz hat eine Wellenlänge von 343 / 100 = 3.43 m oder 343 cm.

Natürlich passen auch Frequenzen mit Vielfachen der Grundwellenlänge zwischen die Wände; man spricht dann von Raum-Moden höherer Ordnung. Die Mode erster Ordnung entsteht bei der Frequenz, deren halbe Wellenlänge dem Abstand zwischen den Wänden entspricht. Das heisst:

f = c / 2d

d ist der Abstand zwischen den Wänden. Ein Beispiel: Ein Raum mit 5 x 4 x 2 Meter Abmassen (L x B x H) erzeugt folgende Moden erster Ordnung zwischen den Wänden:

f1 = 343 / 10 = 34.3 Hz

f2 = 343 / 8 = 42.875 Hz

f3 = 343 / 4 = 85.75 Hz

Sowie die Moden höherer Ordnung, welches ganzzahlige Vielfache der oben genannten Frequenzen sind. Das heisst, für f1 sind dies noch 68.6 Hz, 102.9 Hz, 137.2 Hz usw.

Die Raum-Moden sind die Resonanzfrequenzen des Raumes und verstärken daher diese Frequenzen. Deshalb versucht man die Raum-Moden zu unterdrücken – durch akustische und/oder elektronische Massnahmen. Mehr dazu in Teil 2.

Raum-Moden praktisch ermitteln

Auf dieser Website lassen sich die Raum-Moden für gegebene Räume anzeigen. Es gibt auf der Website ein Fenster «Modes to display». Hier empfehle ich, nur «axial» anzuwählen. Das sind die Moden, die wir oben besprochen haben. Die Moden «tangential» und «oblique» erstrecken sich über 4 bzw. 6 Wände. Sie sind im Pegel wesentlich kleiner als die axialen Moden und daher für unsere Zwecke vernachlässigbar.

Diese Website erlaubt es für schuhschachtelförmige Räume, die Moden zu berechnen. Sind die Räume komplexer, werden diese Berechnungen gegebenenfalls um einiges komplizierter.

Versuchen Sie, anhand dieser Website die Moden Ihres Hörraumes zu ermitteln.

Danach lade ich Sie ein, eines der folgenden Audio-Files herunterzuladen (FLAC oder WAV Format): File 1; File 2

Wenn Sie das File abspielen, werden Sie einen Sinuston hören, der sich in der Frequenz langsam ändert, beginnend mit 200 Hz und endend bei 20 Hz. Achtung, das Signal kann sehr laut sein. Für die Messung genügt eine angenehme Lautstärke.

Versuchen Sie nun mit der Stoppuhr die Zeiten festzuhalten, bei denen die Sinusschwingung am lautesten klingt, das heisst, die Zeiten, bei denen Raum-Moden angeregt werden. Wichtig: Setzen Sie sich dazu an Ihren gewohnten Hörplatz, weil an einem anderen Platz die Raum-Moden völlig unterschiedlich stark in Erscheinung treten können.

Die gemessenen Zeiten können Sie danach anhand dieser Tabelle in die entsprechende Frequenz umrechnen: Die kritischen Frequenzen sollten ungefähr mit den Frequenzen der berechneten Raum-Moden übereinstimmen. Es kann natürlich sein, dass Sie keine überhöhten Frequenzen feststellen können. Das wäre dann ideal – sprich: Ihr Raum ist bezüglich der Raum-Moden neutral. Das ist es, was wir anstreben.